OVERVIEW:
The cost of natural disasters is a major risk for insurers. Recent examples of major catastrophic events, and the associated losses, include Hurricane Katrina ($84 billion), the 2008 Sichuan earthquake ($148 billion), the 2011 Tohoku earthquake and tsunami in Japan (more than $300 billion) and Hurricane Sandy ($75 billion).
Although insurers can transfer risk through reinsurance, there may be limits to capacity, or pricing inefficiencies involved. Catastrophe (CAT) bonds represent an alternative risk transfer mechanism, to transfer insurance risk arising from catastrophes from insurers and reinsurers to the capital market. CAT bonds pay coupons and principal similar to regular bonds, but the payments are contingent; if a pre-specified catastrophic event (the ‘trigger event’) occurs, the repayment of principal (and possibly interest) will be reduced or eliminated. This type of insurance-linked security (ILS) has grown substantially in the past two decades, with over $25 billion outstanding in 2014.
A typical CAT bond transaction is illustrated in Figure 1. The insurer creates a Special Purpose Vehicle (SPV) which acts as a reinsurer for the specific loss covered by the CAT bond. The insurer pays a premium to the SPV. If there is a sufficiently severe catastrophe during the term, the SPV makes a payment to the sponsor to cover the losses arising from the insured event, up to a maximum covered loss.
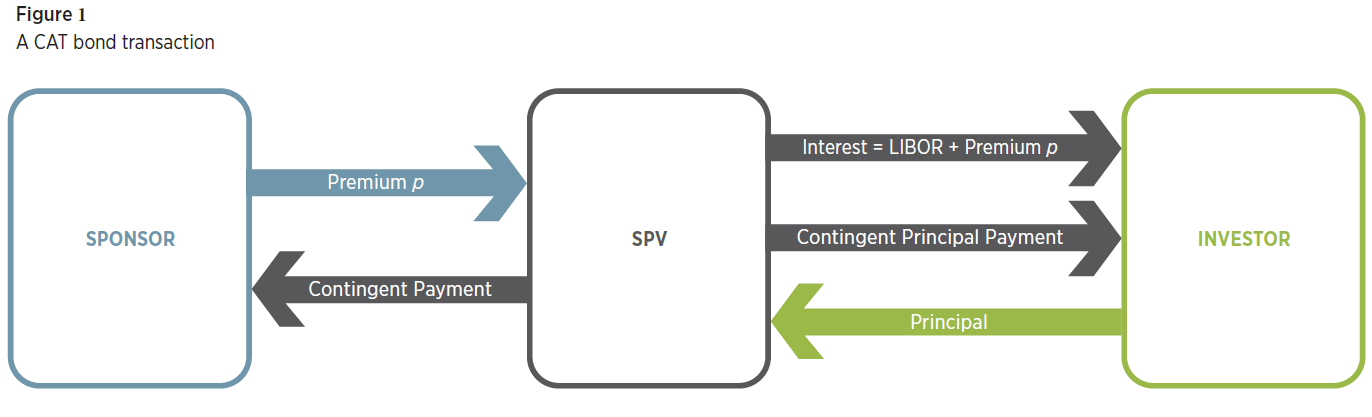
To finance the contingent payment, the SPV sells a CAT bond to investors, who are presumed to be attracted to the investment for its value in diversifying their portfolio (low beta) as well as by the expectation of a high return if the trigger event does not occur. The coupon rate is expressed as LIBOR plus a premium spread. At maturity, if the trigger event has not occurred, the investors receive their full principle back. If the trigger even has occurred, some or all of the principle is paid to the insurers, with the amount dependent on the severity of the event. If any principle remains after reimbursing the insurer, it is returned to the investors.
A commonly used trigger is an indemnity threshold—that is, the payments to the insurer are triggered when a specified catastrophe occurs, with losses exceeding the lower limit specified in the CAT bond prospectus. A parametric trigger uses a physical measure, which can be obtained accurately and immediately after the catastrophic events. This reduces the basis risk and moral hazard and therefore results in a lower premium spread. However, it may not meet the sponsor’s needs, as the payout from the CAT bond is not directly related to the sponsor’s losses. Other trigger types include industry index triggers, where the event depends on the whole industry losses, not just the losses of the sponsoring insurer. This also reduces moral hazard in the contracts.
Pricing the CAT bonds involves setting the premium spread such that the bonds are attractive to investors, and also such that the insurer is provided with catastrophe cover at a reasonable price. The CAT bond prospectus specifies the loss covered, the trigger event, and the maximum loss payable. Investors would also be provided with the insurer’s assessment of the probability that the trigger event will occur (called the probability of first loss or PFL), the probability that the loss will exceed the upper limit (called the probability of last loss or PLL) and the expected proportionate loss, (EL), which is the expected value of the proportion of principle which the investors will lose.
It is important that the calculation of the PFL, PLL and EL are credible to investors. The premium spread relies heavily on the quoted EL. If investors do not trust the models, they will demand higher premium spreads. Extreme value theory (EVT) provides a way to investigate catastrophe risks by utilising the fact that many distributions look similar to each other in the tail of the loss distribution.
A key result from EVT is the Pickands-Balkema-de Haan theorem (see, for example, Embrechts et al., 1997). This theorem is about the ‘excess over threshold’ of a distribution in the right tail. Suppose we set a threshold, d, say, that is far into the tail of the loss distribution for a loss covered by a CAT bond. If the loss arising is a random variable, L, say, then the excess over threshold is the random variable Y, say, which takes the value L – d, provided that L > d and is undefined for L ≤ d. The Pickands-Balkema-de Haan theorem tells us that for most standard distributions in actuarial science and finance the distribution of Y will converge to a Generalized Pareto distribution (GPD) as the threshold moves farther into the tail of the original distribution. The GPD distribution is specified using two parameters, the shape parameter and the scale parameter. When the shape parameter is strictly positive, the GPD is the standard Pareto distribution; when the shape parameter is zero, the GPD is the exponential distribution, and when the shape parameter is negative, the GPD becomes a short tail distribution with a finite upper bound. In each case, the lower bound is 0.
We can use this result by setting the threshold d for defining Y, to be the lower limit for the catastrophe trigger event. In this case, the loss covered by the CAT bond will be Y if Y is less than the upper limit of cover, and it will be the maximum cover if Y is greater than the upper limit. Then we consider what happens if we assume that Y has the GPD distribution — which will be a reasonable assumption provided that the lower limit for cover is sufficiently far into the tail.
The result is a neat functional form for the EL, which demonstrates that the key factors in the evaluation of the EL for high layer CAT bonds are the probability of first loss (PFL), the conditional probability of exhaustion given that a loss arises (PLL/PFL), and the GPD shape parameter.
We can use this result to analyze the statistics provided to investors. We have considered a set of recent CAT bonds covering California earthquake risk. There are 17 of these bond issues in our data set. The PFL’s range from 0.0034 to 0.062, with the more recent issues quoting a higher PFL than the earlier bonds. We use the quoted PLL, PFL, and EL, and solve for the GPD shape parameter. The values range from -21.6 to 4.25. The median value is 0.132. The range is surprising; given that the losses insured are very similar, we would expect the shape parameters to be close. These results suggest a lack of consistency in the evaluation of the PFL, PLL and EL statistics.
When we go further, and analyze the severity data for California earthquakes directly, we find, like others before us, that a negative shape parameter appears to be the best fit to the data.
If the CAT bond issuers are (implicitly) assuming a fatter tailed risk than the true underlying distribution, they may overestimate the PLL, and potentially underestimate the EL. An interesting complication is that the incentive for the sponsor to estimate the EL accurately is not that strong — a more accurate EL, if it is larger, will increase the cost of insuring through the CAT bond.

